LASER ACTION IN C IV PLASMAS

Fig.1 PLASMA DYNAMICS LEADING TO LASER ACTION

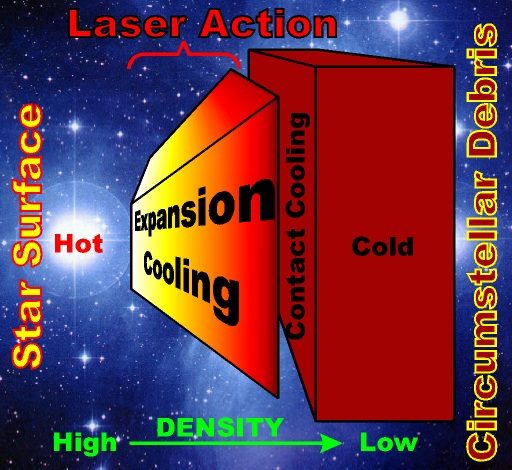
Processes Occurring in Stong Stellar Winds
HOT DENSE PLASMA Highly ionized star atmosphere Composition is often near solar abundances
RAPID EXPANSION
LASER ACTION ZONE Population inversion occurs in this highly ionized but rapidly recombining plasma. A drop by a factor of 5 in temperature corresponds to an adiabatic expansion of volume by 22.
GAS CONTACT COOLING
VERY COLD CIRCUMSTELLAR GAS Low ionization or neutral gas and molecular gas and dust formed from previous plasma ejections. Very efficient heat sink for rapidly cooling the electron temperature of the stellar plasma, laser gain increases dramatically !

IONIZATION EQUILIBRIUM MODEL

The C V Helium-like ion is more energetically stable than other carbon ions because it is a closed shell 'inert gas' configuration of a pair of 1s orbitals. Due to its stability, the C V ion is found over a much larger temperature range, and within a stellar atmosphere, this makes C IV the most likely product when the plasma rapidly cools and collisionally recombines;

      C V  +  e  +  e  ---->  C IV  +  e         Three body recombination
leading to overpopulation of the upper levels of the C IV ion. We thus expect Carbon IV laser transitions to be among the very strongest of laser lines of all the carbon ions. The following table demonstrates the high stability of C V over a very large temperature range,

Non-LTE ionization equilibrium of various carbon ions as a function of temperature for electron densities of 10^15 per cubic centimeter (text version).

and 15 andare treated as grouped into one quantum level

QUANTUM LEVELS OF CARBON IV

Quantum number (n)                                  States with n > 15 are
 inf================================================treated as if they are
  15------------------------------------------------part of the continuum.
  14------------------------------------------------
  13------------------------------------------------States with 9 < n < 16
  12------------------------------------------------have their individual
  11------------------------------------------------angular momenta lumped
  10------------------------------------------------together into hydrogenic
  9s-----  9(l>0)-----------------------------------levels.

  8s-----  8(l>0)-----------------------------------States with 6 < n < 10
                                                    have separate s levels.
  7s-----  7(l>0)-----------------------------------

  6s_____  6p_____  6d_____  6f_____  6g____   6h___Upper laser level
         \/       \/       \/       \/        /
         /\       /\       /\       /\       /
  5s____/  5p____/  5d____/  5f____/  5g____/       Lower laser level

                                                    Diagonal lines indicate
                                                    laser transitions, with
  4s----   4p----   4d----   4f----                 6g->5f being the strongest




           3p----   3d----                          States with n < 7 have
                                                    their angular momentum
  3s----                                            considered separately.


           2p----

  2s---- Ground level

   s=0      p=1      d=2      f=3      g=4      h=5  Angular momentum (L)
The 32 quantum energy levels of C IV used in the collisional-radiative computer simulation of the Lithium-like C IV ion. The vertical axis roughly corresponds to energy and the angular momentum of the state increases towards the right. The criss-cross patterns between levels 5 and 6 represents the laser transitions, the largest population inversion occuring at 6g-5f and 6f-5d.

States with quantum numbers greater than 15 are treated as if they were part of the continuum, states with quantum numbers between 10 and 15 are grouped into one level while the states with n=7,8 and 9 are split into two groups corresponding to core penetrating s states and the remaining angular momenta l>0 are grouped together. All other levels are split into separate states for each n and l.

Transitions with the highest radiative or collisional rate coefficients occur between states differing by one in angular momentum, and as a rule, transitions with smaller energy differences are more likely than transitions with large energy differences. In general three-body recombination occurs into the upper quantum states with a higher probability of large angular momentum quantum number, this partly explains why the 6g-->5f transition is favored among all of the 6 to 5 laser transitions possibilities.

LASER GAIN COMPUTATION

Laser gain diagram for the 6g to 5f transition in the CIV ion (4658 Å) with sudden drop in electron temperature (Te) by a factor of 5 and adiabatic drop by a factor of 11 for the electron density (ne). Gain units in per cm per sec per linewidth (Hz)

The gain is significant only in a very small region of plasma parameter space near ne = 5 X 10^15 cm^-3 and Te = 20,000 K, and decreases very rapidly at high values of ne, it decreases less rapidly at high values of Te, and decreases slowly at high values of Te and low values of ne.

Since the laser gain is very sensitive to the plasma parameters, small changes in the state of a stellar atmosphere over a certain period of time may translate into large changes in laser emission line intensity. This effect has been observed in many quasars.

QUASAR CLASSIFICATION

If the emission line region of a quasar is characterised by a certain electron density (ne) and a certain electron temperature (Te), the sensitivity of the laser gain to these parameters results in large variations in the relative intensities of different laser lines in different quasars, these relative variations are a dominant feature in the spectra of quasars. Partly due to this effect, the amplified spontaneous emission laser lines have been mistakenly identified with extremely redshifted spontaneous emission lines.

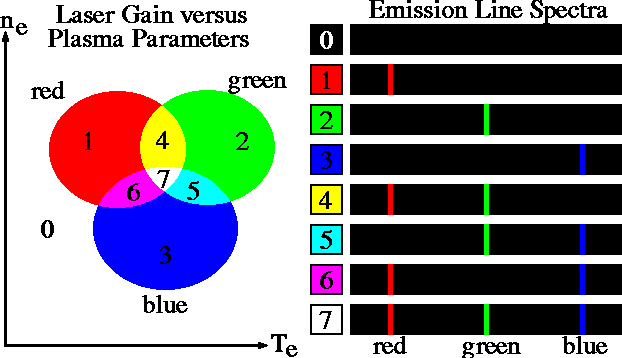
Emission line spectra

The various emission line spectra produced by three laser transitions with slightly different zones of maximum gain in the electron density (ne) electron temperature (Te) parameter space. Spectra corresponding to each numbered region are plotted on the right, demonstrating how large differences in emission line strenghts are produced by small difference in plasma parameters.

The coloured circular regions in the diagram represents strong population inversion for three separate laser transitions; red(1), green(2) or blue(3). The restricted range over which the gain is significant for each respective transition is very narrow in ne, Te parameter space yet some overlap occurs between these regions and is labeled with the colours yellow(4), cyan(5), magenta(6) and white(7). A small difference in the parameters of the stellar atmosphere can lead to very large changes in relative intensity of each laser emission line.

Parameter
Zone		 Emission Lines Present
Red Green Blue
0 No No No
1 Yes No No
2 No Yes No
3 No No Yes
4 Yes Yes No
5 No Yes Yes
6 Yes No Yes
7 Yes Yes Yes
These variations in relative intensities, however, create problems in the spectral classification of quasars. Suppose there are some quasars which show the red, green and blue emission lines (7), some which show only the red and green emission (4), some which show red and blue (6) and some others which show only green and blue (5). It is readily seen that all these four groups have neighbourly positions on the Ne, Te diagram. But in the spectral classification of astronomical objects, usually some criteria are adopted for membership in any spectral class. What do we do in the examples we have given ? Should we say that at least one wavelength should be present say red (arising from a certain transition in a certain ion) must be present in all quasars ? That will leave out groups 2, 3 and 5, even though group 5 is as close to group 4 as group 6 is.

There is, however, a difficulty if we require only one wavelength to be the defining characteristic of a spectral class. Suppose we require that red and green should be present in all quasars belonging to a spectral class. This will then leave out group 3. It is thus seen that there are problems in the spectral classification of quasars. But we must make a start somewhere. We have chosen the requirement that at least two wavelengths must be common in quasars belonging to the same spectral class. In due course, these different spectral classes can be juxtaposed.

Varshni (1977) discusses a quasar spectral class containing two emission lines at about 3820 and 4686 Å, quasars with these two lines are placed into a group called which shares common lines with O VI sequence planetary nuclei and certain emission line stars studied by Sanduleak.

Next Section : Conclusion