CHANCE COINCIDENCES AND THE SO-CALLED REDSHIFT SYSTEMS IN THE ABSORPTION SPECTRUM OF PKS 0237-23

Varshni,Y.P.: 1981, Atrophys.Space Sci., 74, 3.

Also available in Adobe Acrobat PDF format.

1. Introduction

Recently, Boroson et al. (1978, hereafter BSBC) have reported on the absorption spectrum of PKS 0237-23. Six observations made over 3 years were combined to yield wavelengths and equivalent widths of 193 absorption lines in the spectral region 3715-4290 Å. These authors claim that many of these absorption lines are due to C IV 1548.20, 1550.77 Å at various redshifts. A total of 45 redshifts have been claimed.

We have proposed a theory of quasars (Varshni, 1973, 1974a, 1975a, 1977a, b, 1978, 1979. Varshni and Lam, 1976), based on sound physical principles, which does not need the artificial assumption of redshifts and provides satisfactory explanations of the various phenomena associated with quasars. All the observational evidence on quasars either supports our theory, or is consistent with it (Varshni, 1979). Clearly, the claims of BSBC require examination.

2. The 'Redshift' Systems of BSBC

Table I

'Redshifted' C IV doublets in PKS 0237-23

              C IV 1548.20    C IV 1550.77
              ____________    ____________

System              Equivalent       Equiv.          Credibility
number  z       Å   width(Å)   Å     width     R(EW) rating

 1    1.4007  3716.9  0.6     3722.8  0.9      0.67  PO
 2    1.4174  3742.6  0.3     3748.8  0.2      1.50  PO
 3    1.4575  3804.7  0.5     3810.9  0.3      1.67  PO
 3a   1.4794  3838.5  1.2     3845.2  0.1     12.00
 4    1.5023  3874.2  0.7     3880.3  0.7      1.00  C
 4a   1.5063  3880.3  0.7     3886.7  1.9      0.37
 5    1.5144  3892.8  0.8     3899.3  0.3      2.67  PR
 6    1.5153  3894.1  0.4     3900.7  0.3      1.33  PR
 6a   1.5185  3899.3  0.3     3905.5  0.9      0.33
 7    1.5260  3910.8  0.2     3917.1  0.2      1.00  PO
 8    1.5348  3924.6  0.3     3930.8  0.1      3.00  PR
 9    1.5389  3930.8  0.1     3937.2  0.1      1.00  PO
 9a   1.5517  3950.6  1.0     3957.0  0.1     10.00
 10   1.5546  3954.9  0.1     3961.7  0.2      0.50  PO
 11   1.5559  3957.0  0.1     3963.7  0.2      0.50  PR
 12   1.5603  3963.7  0.2     3970.6  0.1      2.00  PR
 12a  1.5787  3992.3  0.1     3999.0  0.1      1.00
 13   1.5950  4017.6  0.7     4024.3  0.3      2.33  C
 13a  1.5956  4018.6  0.4     4025.1  1.2      0.33
 14   1.5964  4019.8  1.2     4026.3  0.8      1.50  C
 15   1.6102  4041.0  0.6     4047.8  0.4      1.50  C
 16   1.6146  4047.8  0.4     4054.8  0.1      4.00  PO
 17   1.6164  4050.6  0.1     4057.6  0.1      1.00  PO
 18   1.6209  4057.6  0.1     4064.4  0.1      1.00  PO
 19   1.6311  4073.4  0.1     4080.4  0.3      0.33  PO
 20   1.6356  4080.4  0.3     4087.2  0.2      1.50  PR
 21   1.6365  4081.7  0.2     4088.7  0.1      2.00  PR
 22   1.6399  4087.2  0.2     4093.9  0.1      2.00  PR
 23   1.6410  4088.7  0.1     4095.7  0.2      0.50  PO
 24   1.6429  4091.7  0.1     4098.5  0.1      1.00  PO
 25   1.6443  4093.9  0.1     4100.7  0.1      1.00  PO
 26   1.6512  4104.5  0.1     4111.4  0.9      0.11  PO
 27   1.6556  4111.4  0.9     4118.2  0.7      1.29  C
 28   1.6568  4113.2  0.9     4120.2  1.1      0.82  C
 29   1.6581  4115.2  0.4     4122.2  0.2      2.00  C
 30   1.6591  4116.9  0.2     4123.7  0.2      1.00  PO
 31   1.6598  4117.7  0.2     4124.8  0.2      1.00  PR
 32   1.6599  4118.2  0.7     4124.8  0.2      3.50  PR
 33   1.6636  4123.7  0.2     4130.7  0.1      2.00  PO
 33a  1.6689  4132.0  0.1     4138.7  0.8      0.13
 34   1.6703  4134.2  0.9     4141.0  1.1      0.82  C
 35   1.6714  4135.9  0.9     4142.7  1.4      0.64  C
 36   1.6732  4138.7  0.8     4145.5  0.4      2.00  C
 37   1.6747  4141.0  1.1     4147.7  0.5      2.20  C
 38   1.6775  4145.5  0.4     4152.1  0.1      4.00  PO
 39   1.6820  4152.1  0.1     4159.3  0.2      0.50  PR
 40   1.6907  4165.6  0.3     4172.8  0.1      3.00  PR
 41   1.7188  4209.3  0.2     4216.1  0.2      1.00  PO
 42   1.7240  4217.4  0.1     4224.1  0.1      1.00  PO
 43   1.7292  4225.3  0.1     4232.1  0.2      0.50  PO
 44   1.7455  4250.6  0.1     4257.6  0.1      1.00  PO
 45   1.7533  4262.6  0.1     4269.7  0.2      0.50  PO

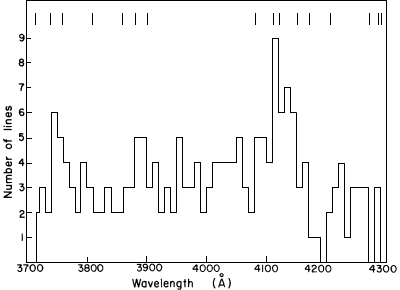
BSBC recognized that many systems could arise by chance, and made a statistical assessment of the overall significance of the identifications. Earlier Varshni (1974b, c, 1975b) had emphasized the importance of taking into account the density distribution of lines for determining chance coincidence "redshifts". Since, in the case of PKS 0237-23, the distribution of lines in wavelength is not uniform, BSBC divided the line list into six 100 Å regions and calculated the expected number of chance C IV doublets in each region by the following formula E(C IV)=[N(N-1)/L](2deltaLambda)(f), where N is the number of lines in the region, L is the extent of the region, deltaLambda is the required accuracy of the separation, and f is the probability of fulfilling the relative equivalent-width criterion by chance. The quantity f was arbitrarily given a value 0.75 by BSBC. We have noted earlier that in the spectrum of PKS 0237-23 there are 52 systems, of which, BSBC have accepted 45. It would be more logical to assume f=45/52=0.87. If the results of BSBC are taken at face value, these indicate that in two wavelength intervals, namely, 4000-4100 Å and 4100-4200 Å, the number of observed systems is much larger than that expected by chance. Taken together, in the two intervals, there are 28 observed systems, whereas 14.1±3.5 are expected by chance.

3. The Error in the Work of BSBC

Fig.1. Number of lines in 10 Å intervals as a function of wavelength for PKS 0237-23. The data are due to BSBC. The vertical bars at the top indicate the positions of the "walls" used in generating the ghost spectra.

The density of lines plays a very important role in determining chance coincidences (Russell and Bowen, 1929. Russell et al., 1944; Varshni (1974b, c, 1975b). The fluctuations in the density of lines in the spectrum of PKS 0237-23 must be properly taken into account in any calculation of the number of chance coincidences.

4. Chance Coincidences

For the mathematically-minded reader, we note that the BSBC procedure is equivalent to calculating

[(Sum from i=1 to m of ai)^2 - (Sum from i=1 to m of ai)]/m

as compared to the correct expression:

Sum from i=1 to m of ai(ai-1),

where ai represents a sequence of numbers. Only if the dispersion in the ai values is very small, the two expressions will be close to each other. If the dispersion in the ai's is large, the former expression can be substantially smaller than the latter one.

The calculated values of P in steps of deltaz=0.002, as a function of z, are shown in Figure 2(a). These values were averaged over deltaz=0.02 and the resulting histogram is shown in Figure 2(b), which may be compared with the results of BSBC, shown in Figure 2(c). The empty squares in Figure 2(c) represent the systems rejected by BSBC. It will be noticed that the chance-coincidence redshift distribution is very similar to that of the actual systems found for PKS 0237-23. We conclude that the proposed systems are consistent with the hypothesis that these are just chance-coincidences without any physical significance.

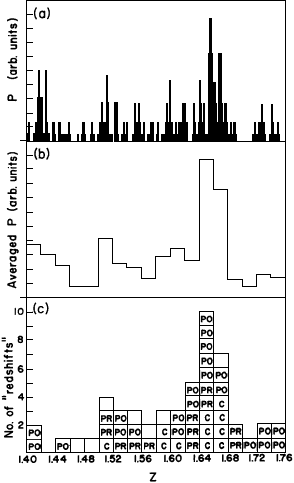
Fig.2. (a) P as a function of z, in steps of deltaz=0.002. (b) Histogram showing averaged P over deltaz=0.02, as function of z. (c) Histogram showing the distribution of absorption redshifts. The credibility rating of the 45 systems of BSBC is indicated by C,PR or PO.

To obtain the actual number of chance-coincidence redshift systems, two methods were used.

Method 1.
A detailed examination of the data of BSBC and Figure 1 shows that the absorption spectrum of PKS 0237-23 can be conveniently divided into 15 intervals, to allow for the varying density of lines, with `walls' at 3715, 3740, 3760, 3810, 3860, 3880, 3900, 4080, 4110, 4120, 4150, 4170, 4205, 4270, 4285, and 4290 Å. Ten ghost spectra (Varshni, 1975b) were generated on a computer (IBM 360/65). The fifteen intervals were considered separately; inside an interval, the ghost wavelengths were generated by the formula

Li(ghost)=Lmin+Ri(Lmax-Lmin),

where Lmin and Lmax represent the lower and upper limits, respectively, of the interval, and Ri is a uniformly distributed random number between zero and one (generated using the RANDU subroutine of IBM's Scientific Subroutine Package). The minimum separation between two lines in the spectrum reported by BSBC is 0.4 Å; it was constrained that the minimum separation between two wavelengths in a ghost spectrum will be the same. The equivalent width of the ith observed line was assigned to Li(ghost). Thus in any given interval, a ghost spectrum has the same number of lines of various equivalent widths as in the observed spectrum. Each ghost spectrum was analysed for `redshifted' C IV doublets such that the separation between the lines is within ±0.33 Å of the correct separation. The initiating number used for RANDU subroutine for generating the ghost spectrum and the total number of C IV doublets found in each of the ten cases are shown in Table II. We have noted earlier that BSBC have not used any well-defined rule for R(EW) for a system to be `acceptable'. For the ghost spectra, we find that if we use the criterion that R(EW) should lie between 0.11 and 5, approximately 85 percent of the systems are `acceptable'. The average total number of chance C IV doublets is 48.5±2.1 and about 85 percent of these are in the `acceptable' category.

Table II

Number of C IV doublets in ghost spectra

Ghost     Initiating  Total
spectrum  number      number of
number    for RANDU   C IV doublets

 1        28471       53
 2        83123       47
 3        26687       45
 4        42003       48
 5        62893       50
 6        66981       49
 7        10737       47
 8        78241       50
 9          137       49
10         8873       47
        Average       48.5±2.1

The next, and more interesting, problem is what are these lines due to. We have succeeded in identifying a good many of the lines recorded by BSBC on the basis of the theory of quasars that we have proposed. We shall present these identifications and the arguments to support them in due course. (in Varshni, 1988)

Acknowledgment. This work was supported in part by a research grant from the Natural Sciences and Engineering Research Council of Canada

References and Related Papers

1. Arp,H.C., Bolton,J.G., Kinman,T.D.: 1967, Astrophys.J., 147, 840.
2. Boksenberg,A., Sargent,W.L.W.: 1975, Astrophys.J., 198, 31.
3. Boroson,T., Sargent,W.L.W., Boksenberg,A., Carswell,R.F.: 1978, Astrophys.J., 220, 772.
4. Burbidge,E.M., Lynds,C.R., Stockton,A.N.: 1968, Astrophys.J., 152, 1077.
5. Greenstein,J.L., Schmidt,M.: 1967, Astrophys.J., 148, L13.
6. Russell,H.N., Bowen,I.S.: 1929, Astrophys.J., 69, 196.
7. Russell,H.N., Moore,C.E., Weeks,D.W.: 1944, Trans.Am.Phil.Soc., 34, 111.
8. Varshni,Y.P.: 1973, Bull.Am.Phys.Soc., 18, 1384.
9. Varshni,Y.P.: 1974a, Bull.Am.Astron.Soc., 6, 213, 308.
10. Varshni,Y.P.: 1974b, Astrophys.J., 193, L5.
11. Varshni,Y.P.: 1974c, Bull.Am.Astron.Soc., 6, 449.
12. Varshni,Y.P.: 1975a, Astrophys.Space Sci., 37, L1.
13. Varshni,Y.P.: 1975b, Astrophys.J., 201, 547.
14. Varshni,Y.P.: 1977a, Astrophys.Space Sci., 46, 443.
15. Varshni,Y.P.: 1977b, J.Roy.Astron.Soc.Canada, 71, 403.
16. Varshni,Y.P.: 1978, in S.Fujita (ed.), The Ta-You Wu Festschrift..Science of Matter, Gordon and Breach, New York, p.285.
17. Varshni,Y.P.: 1979, Phys.Canada, 35, 11.
18. Varshni,Y.P., Lam,C.S.: 1976, Astrophys.Space Sci., 45, 87.